Introduction

Introduction

Genetics4j uses a standard version of Genetic Algorithms. However many steps are highly configurable.

Here is a diagram of the main flow:

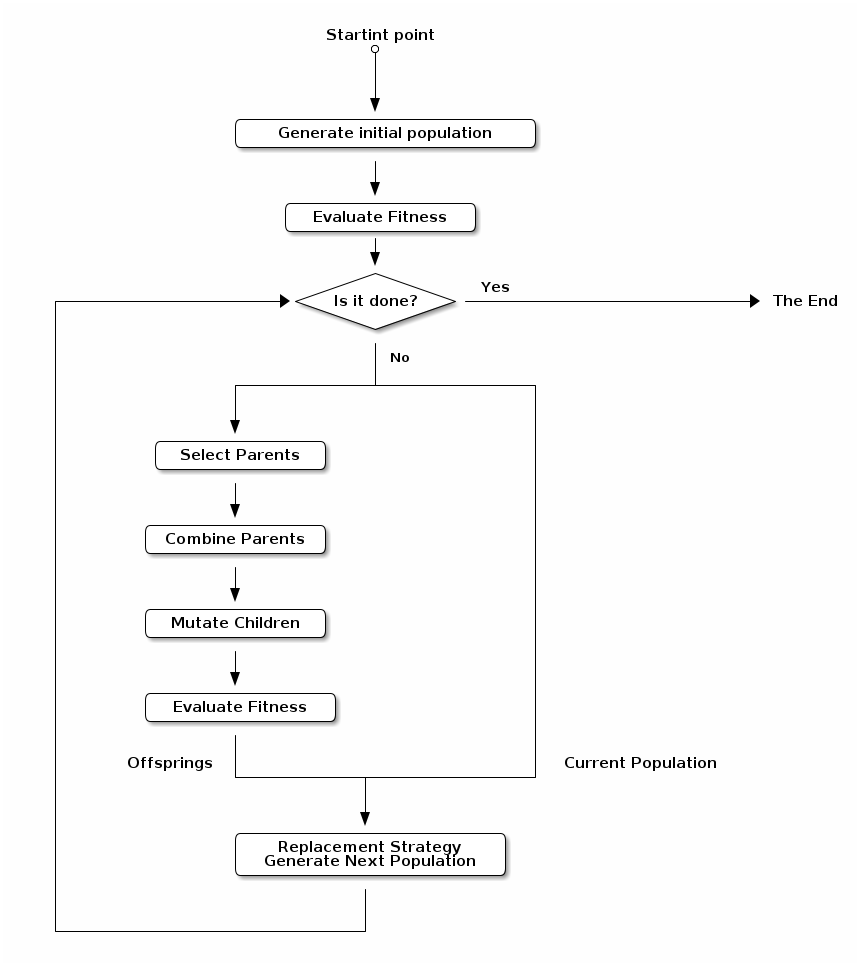
Diagram

This is a standard flow for a genetic algorithm. At each generation, we will select some parents who will then generate some offsprings that will be mutated. And finally, a new generation will be created as defined by the replacement strategy from both offsprings and previous generation. The process will stop as soon as the termination conditions are met.

Concepts

Genotype

An individual, which represent a solution, is called a genotype. A genotype can be composed of multiple chromosomes of different nature. A chromosome can encode data in different ways:

  • Binary representation

  • Integer values

  • Real values

  • Tree

  • Linear sequences (Genetic Programming)

The genotype is defined through the Evolutionary Algorithm Configuration class where one can define the ChromosomeSpecs class

Chromosomes

The core module provides the following types of chromosomes out of the box:

Fitness

Fitness of an individual establish of good of a solution it is. It can be of any type as long as it extends java.lang.Comparable. Which means one could use a Double for a single measure of the fitness as well as more complex data structures for cases such as Multi-Object Optimizations.

The fitness function is established in the EAConfiguration class

Population Generation

Individuals are generated based on their chromosomes' definitions. Each chromosome ships with a default factory. Chromosome factories are defined as ChromosomeFactory, which are configured in the ChromosomeFactoryProvider, which itself is configured in the method chromosomeFactoryProvider() of EAExecutionContext

One could override the way Individuals are generated through either:

Selection Policy

The goal of a SelectionPolicy is to select a set of individuals. It is an important piece of an Evolutionary Algorithm as it helps apply pressure towards the desired goal.

The current set of available selection policies are:

  • DoubleTournament - It implements a double tournament as specified in the paper Fighting Bloat With Nonparametric Parsimony Pressure [fbwnpp]. It is used in Genetic Programming to control bloat by combining tournaments based on fitness with tournaments based on parsimony.

  • MultiSelections - This is a wrapper for combining multiple selection policies. The set of individuals to select will be equally spread across each selection policy

  • MultiTournaments - This operator enables to chain multiple Tournaments

  • ProportionalTournament - It implements a proportional tournament as specified in the paper Fighting Bloat With Nonparametric Parsimony Pressure [fbwnpp]. It is used in Genetic Programming to control bloat by combining tournaments based on fitness with tournaments based on parsimony.

  • RandomSelection - Randomly select individuals with a uniform distribution

  • RouletteWheel - Also called Fitness Proportionate Selection where the probability of selection of an individual is proportionate to its fitness

  • SelectAll - Pass through and will select whatever individuals it can fit in

  • Tournament - It implements k-tournament selection where k invidivuals are picked from the population and the fittest one is selected. Selection pressure will vary bases on the value of k

Combination Policy

The goal of a CombinationPolicy is to combine two individuals and create zero, one or more offsprings.

The current set of available combination policies are:

  • SinglePointCrossover - A random cut is made, separating each parent in half. Offsprings are created by combining each halves

  • MultiPointCrossover - This is an extension of the Single Point Crossover where n cuts are made and the offsprings are created by combining each sections

  • OrderCrossover (OX) - This operator assumes a path representation in the chromosome and construct an offspring by selecting a subtour in one parent and preserving the relative order of the other parent. This is only available for chromosomes of type IntChromosomeSpec

  • PickFirstParent - The first parent is always chosen as the offspring

  • EdgeRecombinationCrossover (ERX) - This operator assumes a path representation in the chromosome and construct an offspring with the aim of preserving the edges from the parents as much as possible. This is only available for chromosomes of type IntChromosomeSpec

  • MultiCombinations- This is a wrapper for combining multiple combination policies. It will select a combination policy randomly with a uniform distribution

Mutation

The goal of a MutationPolicy is to maintain diversity and allow undirected jumps to slightly different areas of the search space.

The current set of available mutation policies are:

  • RandomMutation - Randomly change a value of the chromosomes. It might be flipping bits in the case of bit chromosomes or changing to a different value for int chromosomes

  • SwapMutation - Randomly change two values of the chromosomes

  • PartialMutation - Apply a MutationPolicy for a very specific chromosome of the genotype

  • MultiMutation - This is a wrapper for combining multiple mutation policies. It will select a mutation policy randomly with a uniform distribution

Termination

Termination responsibility is determine whether or not the evolution process should continue or not. Termination conditions could be based on any criteria, be it computation time, diversity in the population, reaching a specific fitness value or a combination of those.

Terminations is a helper class which provides a few out of the box helpful termination conditions.

Replacement Strategy

The replacement strategy is crucial for driving the process as it specifies how to generate the next generation based on the current population and the offsprings.

The current set of available replacement strategies are:

  • Elitism - The best individuals of respectively, the current generation and the mutated offsprings, are retained for the next generation.

  • GenerationalReplacement - The best individuals of the mutated offsprings are retained for the next generation and the current population is discarded.

  • DeleteNLast - The N weakest invidivuals of the current population are discarded and replaced by the best offsprings.

References

  • [fbwnpp] Sean Luke, Liviu Panait. Fighting Bloat With Nonparametric Parsimony Pressure