final Builder programBuilder = ImmutableProgram.builder();
programBuilder.addFunctions(Functions.ADD, Functions.MUL, Functions.DIV, Functions.SUB, Functions.POW);
programBuilder.addTerminal(Terminals.InputDouble(random), Terminals.CoefficientRounded(random, -10, 10));
programBuilder.inputSpec(ImmutableInputSpec.of(List.of(Double.class)));
programBuilder.maxDepth(4);
final Program program = programBuilder.build();6 ways to handle your bloat issues
Table of Contents
Preface
All the executions and plots are generated from scratch at build time. This means results may vary from execution to execution.
This also creates some constraints in terms of execution time. A proper analysis would have us execute each approach many times prior to making any generalization, which we cannot afford here.
While I could use the same seed for the random generator and therefore generate reproducible results, this wouldn’t be befitting of a demonstration of evolutionary algorithms.
Note also the purpose of this document is to serve me as notes and is not meant to be taken as exhaustive or a fully fledged blog post.
Introduction
Bloat is a well known problem when using Genetic Programming where programs will grow over time without significant improvement to the fitness. Consequently many methods have been devised to combat bloat and we will review a few of them.
Methodology
We will try all the methods on a symbolic regression of the equation:
\$f(x) = 6*x^2 - x + 8\$
This means we will generate 100 examples of data points (x, f(x)) and use Genetic Programming to rediscover the equation which generated them. In a real setting, we would obviously not know the original equation.
The generated programs are defined by the following specification:
As you can see, programs will take a double as an input, which will be considered as a given x for the equation.
It is not visible in the snippet above, but unless told otherwise, we will use populations of 500 individuals for our experiments.
Given that we will need to process the output of each generation in order to plot meaningful information, we will define a general CSV logger which will also record the rank of each individual comparing to the pareto frontier:
public static <T extends Comparable<T>> EvolutionListener<T> csvLogger(final String filename,
final Function<EvolutionStep<T, List<Set<Integer>>>, Double> computeScore,
final Function<EvolutionStep<T, List<Set<Integer>>>, Double> computeComplexity,
final BiFunction<List<Genotype>, List<T>, List<FitnessVector<Double>>> convert2FitnessVector) {
Validate.isTrue(StringUtils.isNotBlank(filename));
Validate.notNull(computeScore);
Validate.notNull(computeComplexity);
return CSVEvolutionListener.<T, List<Set<Integer>>>of(filename, (generation, population, fitness, isDone) -> {
final List<FitnessVector<Double>> fitnessAndSizeVectors = convert2FitnessVector.apply(population, fitness);
return ParetoUtils.rankedPopulation(Comparator.<FitnessVector<Double>>reverseOrder(),
fitnessAndSizeVectors); (1)
},
List.of(ColumnExtractor.of("generation", evolutionStep -> evolutionStep.generation()),
ColumnExtractor.of("score", evolutionStep -> computeScore.apply(evolutionStep)),
ColumnExtractor.of("complexity", evolutionStep -> computeComplexity.apply(evolutionStep)),
ColumnExtractor.of("rank", evolutionStep -> {
final List<Set<Integer>> rankedPopulation = evolutionStep.context().get();
Integer rank = null;
for (int i = 0; i < 5 && i < rankedPopulation.size() && rank == null; i++) {
if (rankedPopulation.get(i).contains(evolutionStep.individualIndex())) {
rank = i;
}
}
return rank != null ? rank : -1;
}),
ColumnExtractor.of("expression",
evolutionStep -> TreeNodeUtils.toStringTreeNode(evolutionStep.individual(), 0)))
);
}| 1 | We are ranking the whole population and using that information as context for each ColumnExtractor |
Methods
Tarpeian Method
The tarpeian method is about minimizing the fitness of individuals with larger than average size. Only a percentage of the targeted individuals are affected as a way to modulate the intensity of the pressure.
In this case, the fitness will be defined as the Mean Squared Error over a given set of input, with a large penalty for not-finite results. This implies the smaller the fitness, the better the fit and the individual:
final Fitness<Double> computeFitness = (genoType) -> {
final TreeChromosome<Operation<?>> chromosome = (TreeChromosome<Operation<?>>) genoType.getChromosome(0);
final Double[][] inputs = new Double[100][1];
for (int i = 0; i < 100; i++) {
inputs[i][0] = (i - 50) * 1.2;
}
double mse = 0;
for (final Double[] input : inputs) {
final double x = input[0];
final double expected = SymbolicRegressionUtils.evaluate(x);
final Object result = ProgramUtils.execute(chromosome, input);
if (Double.isFinite(expected)) {
final Double resultDouble = (Double) result;
mse += Double.isFinite(resultDouble) ? (expected - resultDouble) * (expected - resultDouble)
: 1_000_000_000;
}
}
return Double.isFinite(mse) ? mse / 100.0 : Double.MAX_VALUE;
};Here is the configuration we use:
final var eaConfigurationBuilder = new EAConfiguration.Builder<Double>();
eaConfigurationBuilder.chromosomeSpecs(ProgramTreeChromosomeSpec.of(program)) (1)
.parentSelectionPolicy(Tournament.of(3))
.combinationPolicy(ProgramRandomCombine.build())
.mutationPolicies(ProgramRandomMutate.of(0.10),
ProgramRandomPrune.of(0.12),
NodeReplacement.of(0.05),
ProgramApplyRules.of(SimplificationRules.SIMPLIFY_RULES))
.optimization(Optimization.MINIMIZE) (2)
.postEvaluationProcessor(TarpeianMethod.ofTreeChromosome(random, 0, 0.3, Double.MAX_VALUE)) (3)
.termination(or(ofMaxGeneration(200), ofFitnessAtMost(0.00001d)))
.fitness(computeFitness);
final EAConfiguration<Double> eaConfiguration = eaConfigurationBuilder.build();| 1 | We only use a program chromosome |
| 2 | We do want to minize the fitness as it means less errors from the individuals |
| 3 | Tarpeian Method defined as a post evaluation processor to re-evaluate their fitness. We will only affect 30% of the individuals above average and set their fitness to Double.MAX_VALUE |
Here are some plots of an execution:
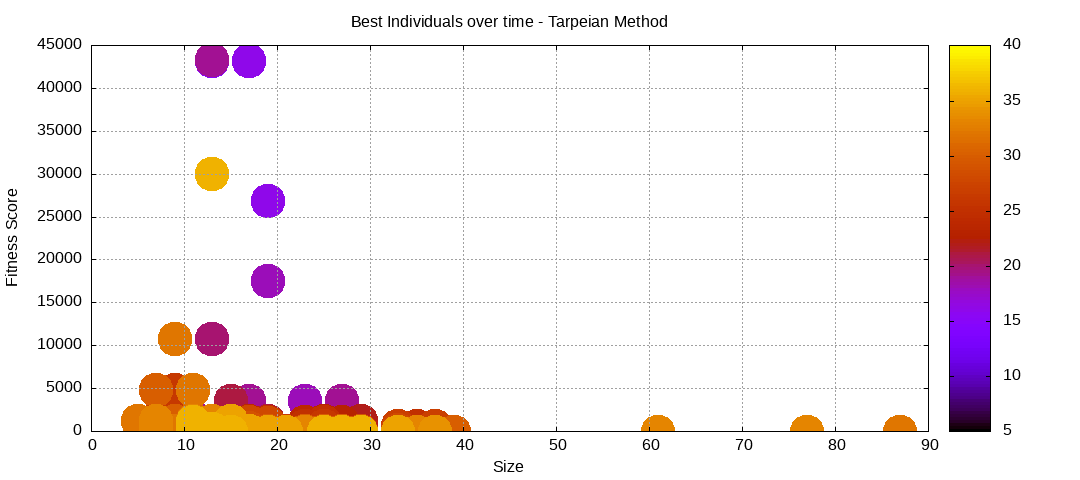
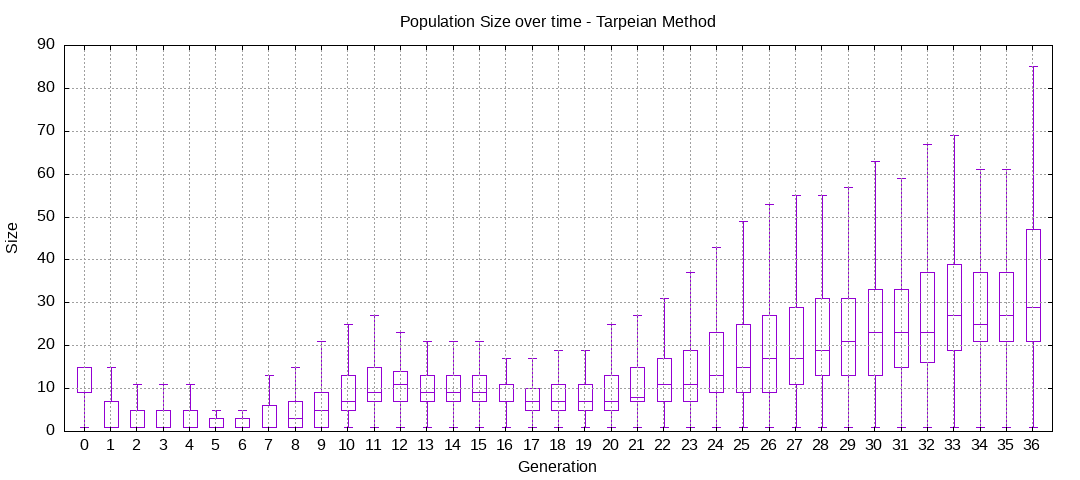
We should observe better fitness over time as well as a containment of the population size.
Constant Parsimony Pressure
Constant Parsimony Pressure attempts to control bloat by assigning a penalty based on the size of a given individual. This imply that given identical results of two programs, the one with the smaller size shall be considered as having a better fitness.
In this case, the fitness will be defined as the Mean Squared Error over a given set of input, along with an additional penalty based on its size and possibly an additional large penalty for not-finite results. This implies the smaller the error and the program, the better the fit and the individual:
final Fitness<Double> computeFitness = (genoType) -> {
final TreeChromosome<Operation<?>> chromosome = (TreeChromosome<Operation<?>>) genoType.getChromosome(0);
final Double[][] inputs = new Double[100][1];
for (int i = 0; i < 100; i++) {
inputs[i][0] = (i - 50) * 1.2;
}
double mse = 0;
for (final Double[] input : inputs) {
final double x = input[0];
final double expected = SymbolicRegressionUtils.evaluate(x);
final Object result = ProgramUtils.execute(chromosome, input);
if (Double.isFinite(expected)) {
final Double resultDouble = (Double) result;
mse += Double.isFinite(resultDouble) ? (expected - resultDouble) * (expected - resultDouble)
: 1_000_000_000;
}
}
return Double.isFinite(mse) ? mse / 100.0 + 1.5 * chromosome.getSize() : Double.MAX_VALUE; (1)
};| 1 | We add \$1.5 * "chromosome.getSize()"\$ to the MSE |
Here is the configuration we use:
final var eaConfigurationBuilder = new EAConfiguration.Builder<Double>();
eaConfigurationBuilder.chromosomeSpecs(ProgramTreeChromosomeSpec.of(program)) (1)
.parentSelectionPolicy(Tournament.of(3))
.combinationPolicy(ProgramRandomCombine.build())
.mutationPolicies(ProgramRandomMutate.of(0.10),
ProgramRandomPrune.of(0.12),
NodeReplacement.of(0.05),
ProgramApplyRules.of(SimplificationRules.SIMPLIFY_RULES))
.optimization(Optimization.MINIMIZE) (2)
.termination(or(ofMaxGeneration(200), ofFitnessAtMost(20.0d))) (3)
.fitness(computeFitness);
final EAConfiguration<Double> eaConfiguration = eaConfigurationBuilder.build();| 1 | We only use a program chromosome |
| 2 | We do want to minize the fitness as it means less errors from the individuals as well as a smaller size |
| 3 | Note that no termination condition can expect to ever reach a fitness of 0 as there will always be a cost for the program size |
Here are some plots of an execution:
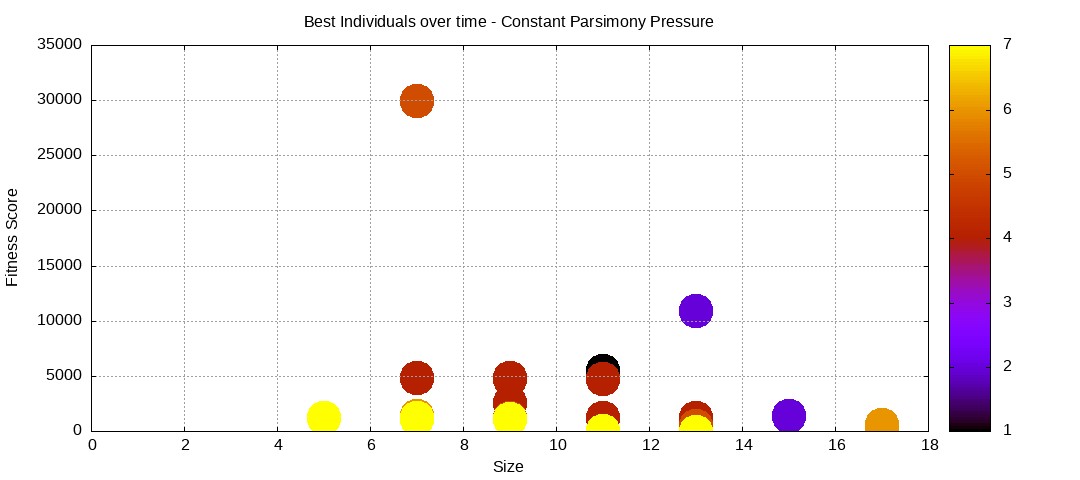
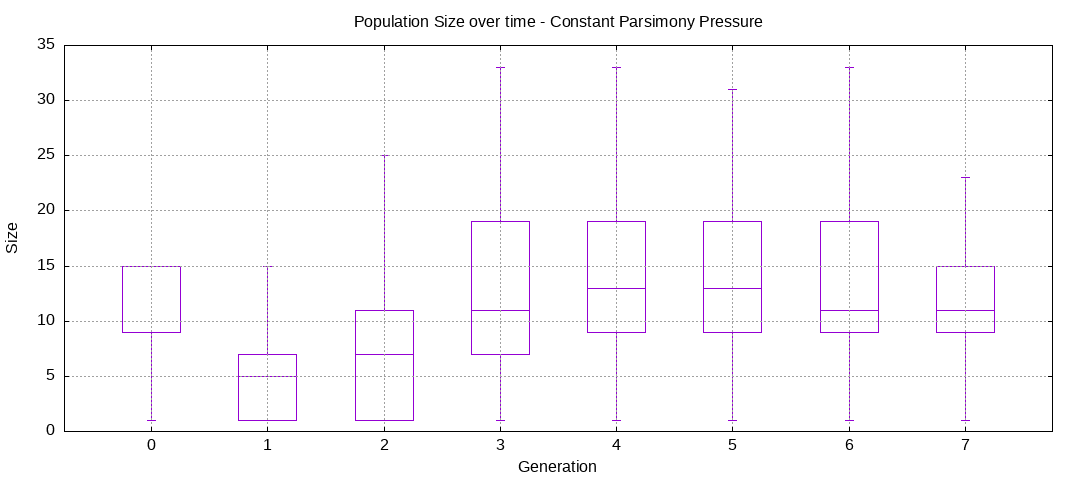
We should observe better fitness over time as well as a containment of the population size.
Double Tournaments
Double Tournaments add some additional pressure to the selection process by combining two tournaments, one after the other:
-
One tournament based on fitness
-
One tournament based on program size
The order of the tournaments didn’t seem to matter by the authors of that method. However they did find that even using a program size tournament of 2 was too much pressure for the evolution process. To reduce that pressure, they made it probabilistic.
Note that given the tournaments are combined, this means each candidate of the second tournament is the result of a tournament, the first one.
Since this method is based on improving the selection process, it means the computation of the fitness is the most straightforward and only focuses on the MSE:
final Fitness<Double> computeFitness = (genoType) -> {
final TreeChromosome<Operation<?>> chromosome = (TreeChromosome<Operation<?>>) genoType.getChromosome(0);
final Double[][] inputs = new Double[100][1];
for (int i = 0; i < 100; i++) {
inputs[i][0] = (i - 50) * 1.2;
}
double mse = 0;
for (final Double[] input : inputs) {
final double x = input[0];
final double expected = SymbolicRegressionUtils.evaluate(x);
final Object result = ProgramUtils.execute(chromosome, input);
if (Double.isFinite(expected)) {
final Double resultDouble = (Double) result;
mse += Double.isFinite(resultDouble) ? (expected - resultDouble) * (expected - resultDouble)
: 1_000_000_000;
}
}
return Double.isFinite(mse) ? mse / 100.0d : Double.MAX_VALUE;
};The definition of the double tournament is also straightforward:
final Comparator<Individual<Double>> parsimonyComparator = (a, b) -> {
final TreeChromosome<Operation<?>> treeChromosomeA = a.genotype()
.getChromosome(0, TreeChromosome.class);
final TreeChromosome<Operation<?>> treeChromosomeB = b.genotype()
.getChromosome(0, TreeChromosome.class);
return Integer.compare(treeChromosomeA.getSize(), treeChromosomeB.getSize());
};
final DoubleTournament<Double> doubleTournament = DoubleTournament
.of(Tournament.of(3), parsimonyComparator, 1.1d);Here is the configuration we use:
final var eaConfigurationBuilder = new EAConfiguration.Builder<Double>();
eaConfigurationBuilder.chromosomeSpecs(ProgramTreeChromosomeSpec.of(program)) (1)
.parentSelectionPolicy(doubleTournament)
.replacementStrategy(Elitism.builder() (2)
.offspringRatio(0.99)
.offspringSelectionPolicy(doubleTournament)
.survivorSelectionPolicy(doubleTournament)
.build())
.combinationPolicy(ProgramRandomCombine.build())
.mutationPolicies(ProgramRandomMutate.of(0.10),
ProgramRandomPrune.of(0.12),
NodeReplacement.of(0.05),
ProgramApplyRules.of(SimplificationRules.SIMPLIFY_RULES))
.optimization(Optimization.MINIMIZE) (3)
.termination(or(ofMaxGeneration(200), ofFitnessAtMost(0.00001)))
.fitness(computeFitness);
final EAConfiguration<Double> eaConfiguration = eaConfigurationBuilder.build();| 1 | We only use a program chromosome |
| 2 | We need to override the default replacement strategy to make use of our double tournament |
| 3 | We do want to minize the fitness as it means less errors from the individuals |
Here are some plots of an execution:
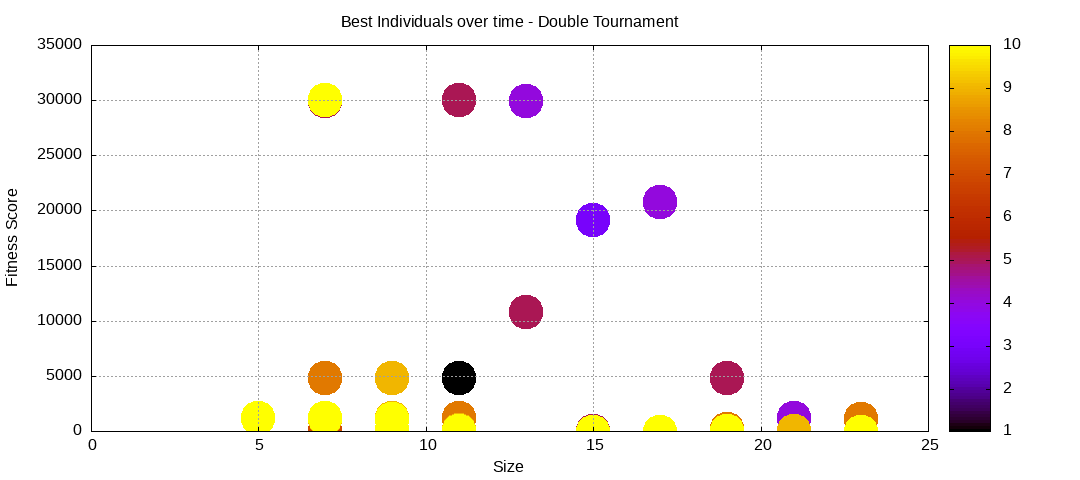
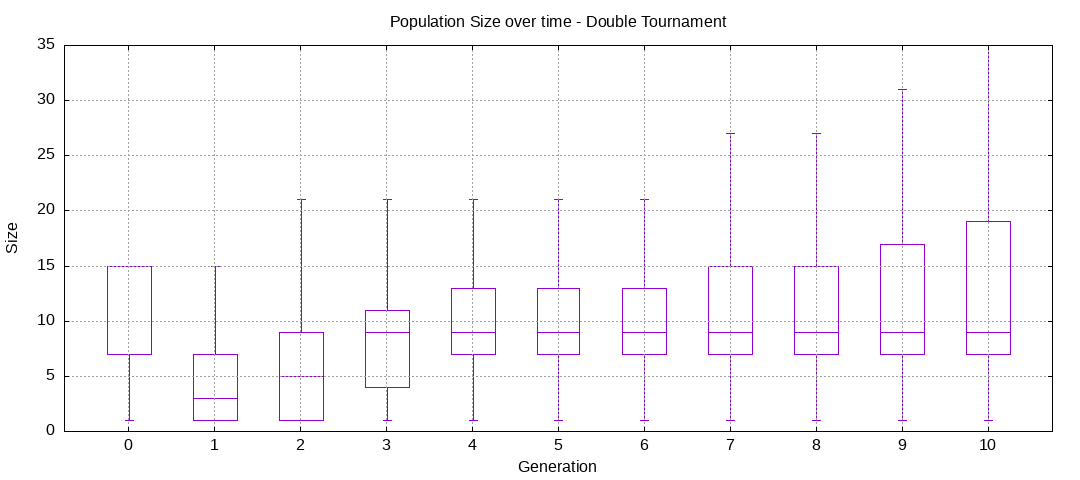
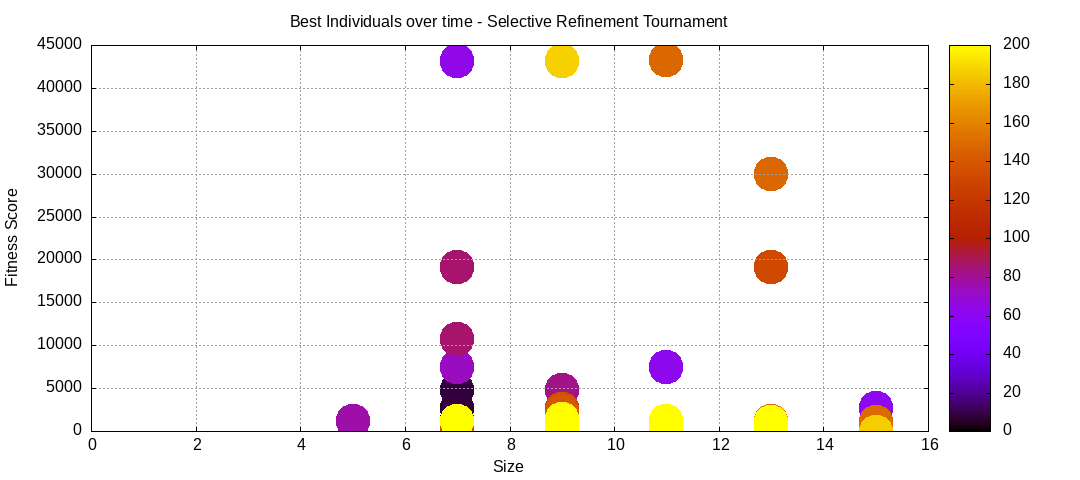
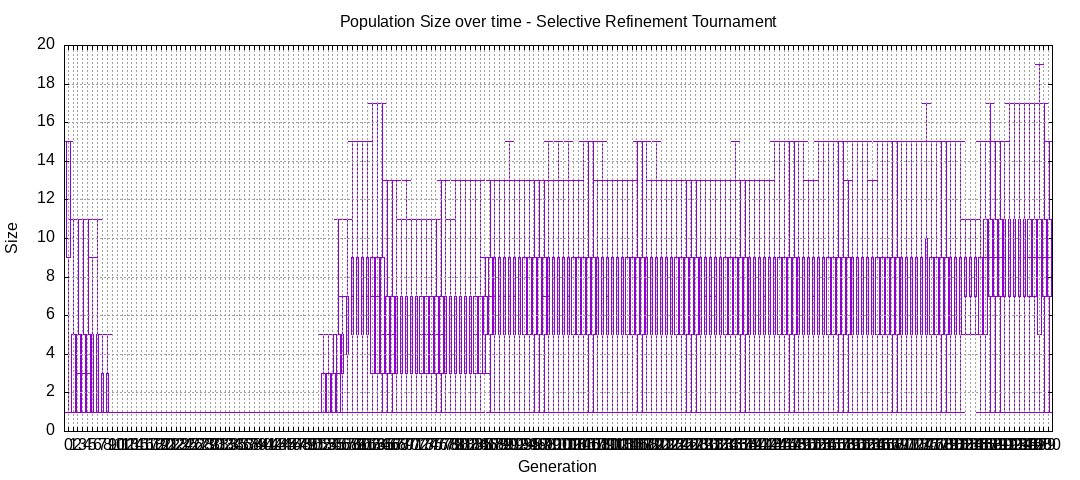
We should observe better fitness over time as well as a containment of the population size.
Proportional Tournaments
Proportional Tournaments are a variant of Double Tournaments where there is only one tournament, chosen between two possible tournaments with some degree of probability.
Since this method is based on improving the selection process like the double tournament method, it means the computation of the fitness is the most straightforward and only focuses on the MSE:
final Fitness<Double> computeFitness = (genoType) -> {
final TreeChromosome<Operation<?>> chromosome = (TreeChromosome<Operation<?>>) genoType.getChromosome(0);
final Double[][] inputs = new Double[100][1];
for (int i = 0; i < 100; i++) {
inputs[i][0] = (i - 50) * 1.2;
}
double mse = 0;
for (final Double[] input : inputs) {
final double x = input[0];
final double expected = SymbolicRegressionUtils.evaluate(x);
final Object result = ProgramUtils.execute(chromosome, input);
if (Double.isFinite(expected)) {
final Double resultDouble = (Double) result;
mse += Double.isFinite(resultDouble) ? (expected - resultDouble) * (expected - resultDouble)
: 1_000_000_000;
}
}
return Double.isFinite(mse) ? mse / 100.0d : Double.MAX_VALUE;
};The definition of the proportional tournament is also straightforward. We will use two tournaments, one for the fitness and the other for the parsimony:
final Comparator<Individual<Double>> parsimonyComparator = (a, b) -> {
final TreeChromosome<Operation<?>> treeChromosomeA = a.genotype()
.getChromosome(0, TreeChromosome.class);
final TreeChromosome<Operation<?>> treeChromosomeB = b.genotype()
.getChromosome(0, TreeChromosome.class);
return Integer.compare(treeChromosomeA.getSize(), treeChromosomeB.getSize());
};
final ProportionalTournament<Double> proportionalTournament = ProportionalTournament
.of(3, 0.65, Comparator.comparing(Individual::fitness), parsimonyComparator);Here is the configuration we use:
final var eaConfigurationBuilder = new EAConfiguration.Builder<Double>();
eaConfigurationBuilder.chromosomeSpecs(ProgramTreeChromosomeSpec.of(program)) (1)
.parentSelectionPolicy(proportionalTournament)
.replacementStrategy(Elitism.builder() (2)
.offspringRatio(0.99)
.offspringSelectionPolicy(proportionalTournament)
.survivorSelectionPolicy(proportionalTournament)
.build())
.combinationPolicy(ProgramRandomCombine.build())
.mutationPolicies(ProgramRandomMutate.of(0.10),
ProgramRandomPrune.of(0.12),
NodeReplacement.of(0.05),
ProgramApplyRules.of(SimplificationRules.SIMPLIFY_RULES))
.optimization(Optimization.MINIMIZE) (3)
.termination(or(ofMaxGeneration(200), ofFitnessAtMost(0.00001)))
.fitness(computeFitness);
final EAConfiguration<Double> eaConfiguration = eaConfigurationBuilder.build();| 1 | We only use a program chromosome |
| 2 | We need to override the default replacement strategy to make use of our proportional tournament |
| 3 | We do want to minize the fitness as it means less errors from the individuals |
Here are some plots of an execution:
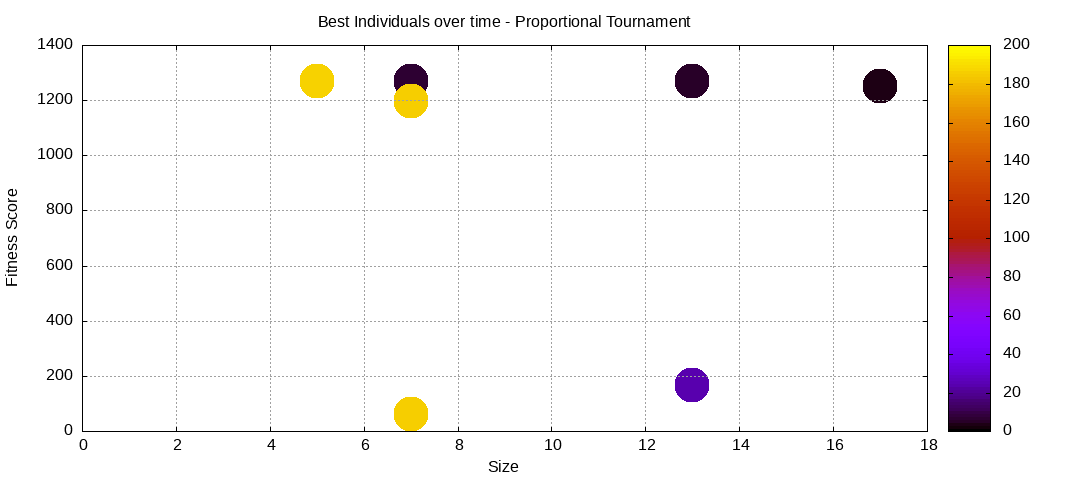
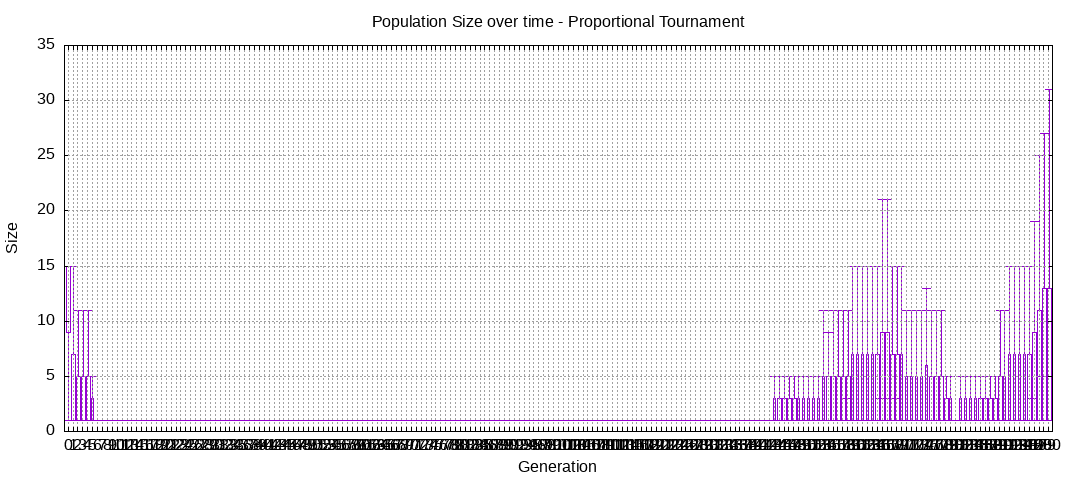
We should observe better fitness over time as well as a containment of the population size. However it will also fail quite frequently to find any solution, which would be translated in the plots above with a lack of clear progression with the front as well as reaching the maximum allowed number of generations, which is 200.
Multi Objective Optimization with NSGA2
This approach decompose the fitness in multiple objectives:
-
Fitness of an individual
-
Parsimony
Nondominated Sorting Genetic Algorithm II (NSGA-II), is an algorithms used to apply some selection pressure.
Since we are working on a Multi Objective Optimization problem, this changes our fitness computation a bit. It will now return a FitnessVector, separating each component in their own dimension:
final Fitness<FitnessVector<Double>> computeFitness = (genoType) -> {
final TreeChromosome<Operation<?>> chromosome = (TreeChromosome<Operation<?>>) genoType.getChromosome(0);
final Double[][] inputs = new Double[100][1];
for (int i = 0; i < 100; i++) {
inputs[i][0] = (i - 50) * 1.2;
}
double mse = 0;
for (final Double[] input : inputs) {
final double x = input[0];
final double expected = SymbolicRegressionUtils.evaluate(x);
final Object result = ProgramUtils.execute(chromosome, input);
if (Double.isFinite(expected)) {
final Double resultDouble = (Double) result;
if (Double.isFinite(resultDouble)) {
mse += (expected - resultDouble) * (expected - resultDouble);
} else {
mse += 1_000_000_000;
}
}
}
return Double.isFinite(mse) ? new FitnessVector<Double>(mse / 100.0,
(double) chromosome.getRoot()
.getSize())
: new FitnessVector<Double>(Double.MAX_VALUE, Double.MAX_VALUE);
};The configuration doesn’t require much change as Genetics4j provides support for NSGA2 through selection:
final var eaConfigurationBuilder = new EAConfiguration.Builder<FitnessVector<Double>>();
eaConfigurationBuilder.chromosomeSpecs(ProgramTreeChromosomeSpec.of(program)) (1)
.parentSelectionPolicy(TournamentNSGA2Selection.ofFitnessVector(2, 3, deduplicator)) (2)
.replacementStrategy(Elitism.builder() (3)
.offspringRatio(0.995)
.offspringSelectionPolicy(TournamentNSGA2Selection.ofFitnessVector(2, 3, deduplicator))
.survivorSelectionPolicy(NSGA2Selection.ofFitnessVector(2, deduplicator))
.build())
.combinationPolicy(ProgramRandomCombine.build())
.mutationPolicies(MultiMutations
.of(ProgramRandomMutate.of(0.15 * 3), ProgramRandomPrune.of(0.15 * 3), NodeReplacement.of(0.15 * 3)),
ProgramApplyRules.of(SimplificationRules.SIMPLIFY_RULES))
.optimization(Optimization.MINIMIZE)
.termination(Terminations.or(Terminations.<FitnessVector<Double>>ofMaxGeneration(200),
(eaConfiguration, generation, population, fitness) -> fitness.stream()
.anyMatch(fv -> fv.get(0) <= 0.000001 && fv.get(1) <= 20))) (4)
.fitness(computeFitness);
final EAConfiguration<FitnessVector<Double>> eaConfiguration = eaConfigurationBuilder.build();| 1 | We only use a program chromosome |
| 2 | We need to override the parent selection strategy to make use of our NSGA2 based tournaments |
| 3 | We need to override the default replacement strategy to make use of our NSGA2 based tournaments |
| 4 | We do have to separate the objectives when checking for termination |
The astute reader will also notice the presence of a deduplicator when configuring the NSGA2 tournaments. A deduplicator is optional and a function indicating if two individuals represent the same thing.
However I noticed a definitive improvement in the results with this approach as it limits the impact of the individuals at the corners in the front. Without it, the population would rapidly be overrun by individuals with poor fitness but of size 1 as no other individual could dominate them. Removing duplicates helps applying continuous pressure from the front and reducing the impact of close but not identical individuals.
The execution context is created through a helper class:
final var eaExecutionContextBuilder = GPEAExecutionContexts.<FitnessVector<Double>>forGP(random);Also of note that it is easy to add support for MOO as the relevant code is automatically loaded and made available as long as it can be located on the classpath.
Here are some plots of an execution:
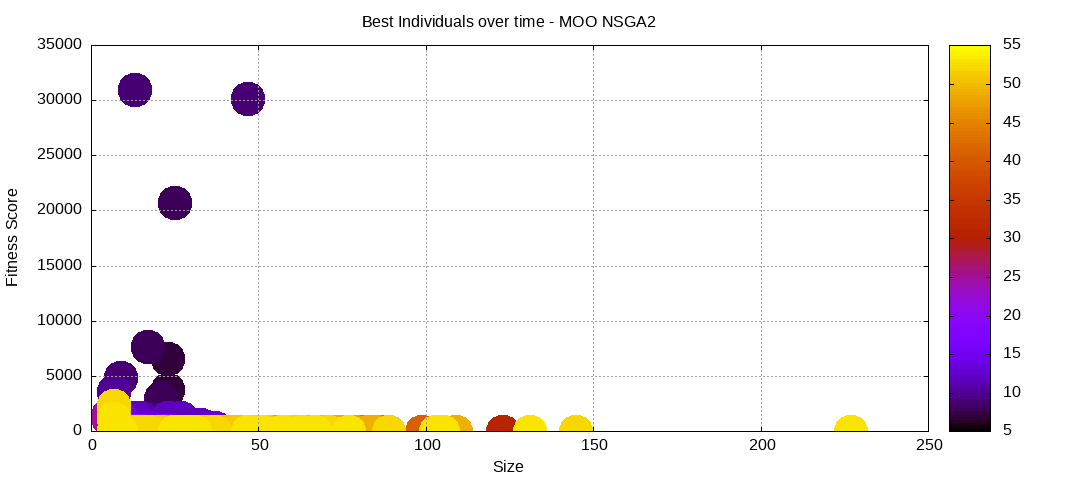
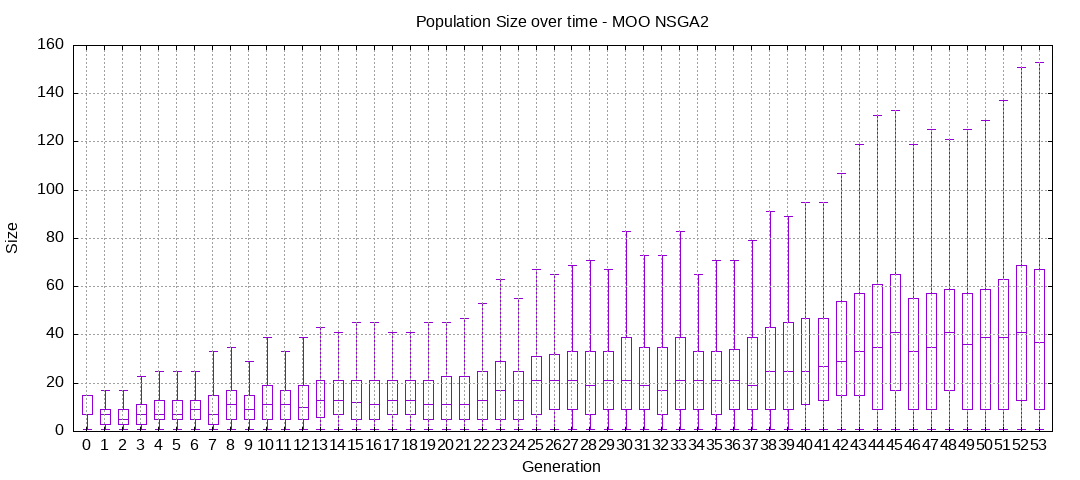
We should observe better fitness over time as well as a containment of the population size.
Multi Objective Optimization with SPEA2
Similarly to NSGA2, the Strength Pareto Evolutionary Algorithm 2 (SPEA2), is geared towards Multi Objective Optimization problems. Due to the specificites of the implementations in the orignal paper, SPEA2 is implemented as a replacement strategy where the archive is represented by the selected population. However we can’t use the SPEA2 fitness to select parents as we do not have that information at that step and it would not work with the actual fitness used to measure the individuals.
Since we are working on a Multi Objective Optimization problem, this doesn’t change at all our fitness evaluation comparing to the previous approach. It still returns a FitnessVector, separating each component in their own dimension:
final Fitness<FitnessVector<Double>> computeFitness = (genoType) -> {
final TreeChromosome<Operation<?>> chromosome = (TreeChromosome<Operation<?>>) genoType.getChromosome(0);
final Double[][] inputs = new Double[100][1];
for (int i = 0; i < 100; i++) {
inputs[i][0] = (i - 50) * 1.2;
}
double mse = 0;
for (final Double[] input : inputs) {
final double x = input[0];
final double expected = SymbolicRegressionUtils.evaluate(x);
final Object result = ProgramUtils.execute(chromosome, input);
if (Double.isFinite(expected)) {
final Double resultDouble = (Double) result;
if (Double.isFinite(resultDouble)) {
mse += (expected - resultDouble) * (expected - resultDouble);
} else {
mse += 1_000_000_000;
}
}
}
return Double.isFinite(mse) ? new FitnessVector<Double>(mse / 100.0,
(double) chromosome.getRoot()
.getSize())
: new FitnessVector<Double>(Double.MAX_VALUE, Double.MAX_VALUE);
};The configuration doesn’t require much change as Genetics4j provides support for NSGA2 through selection. We will also take advantage of NSGA2 to select the parents:
final var eaConfigurationBuilder = new EAConfiguration.Builder<FitnessVector<Double>>();
eaConfigurationBuilder.chromosomeSpecs(ProgramTreeChromosomeSpec.of(program)) (1)
.parentSelectionPolicy(TournamentNSGA2Selection.ofFitnessVector(2, 3, deduplicator)) (2)
.replacementStrategy(SPEA2Replacement.ofFitnessVector(deduplicator)) (3)
.combinationPolicy(ProgramRandomCombine.build())
.mutationPolicies(MultiMutations
.of(ProgramRandomMutate.of(0.15 * 3), ProgramRandomPrune.of(0.15 * 3), NodeReplacement.of(0.15 * 3)),
ProgramApplyRules.of(SimplificationRules.SIMPLIFY_RULES))
.optimization(Optimization.MINIMIZE)
.termination(Terminations.or(Terminations.<FitnessVector<Double>>ofMaxGeneration(200),
(eaConfiguration, generation, population, fitness) -> fitness.stream()
.anyMatch(fv -> fv.get(0) <= 0.00001 && fv.get(1) <= 20)))
.fitness(computeFitness);
final EAConfiguration<FitnessVector<Double>> eaConfiguration = eaConfigurationBuilder.build();| 1 | We only use a program chromosome |
| 2 | We need to override the parent selection strategy to make use of our NSGA2 based tournaments |
| 3 | We need to override the default replacement strategy to make use of SPEA2 |
Similarly to NSGA2, SPEA2 can benefit from deduplicating the solutions and we do make use of it here.
Here are some plots of an execution:
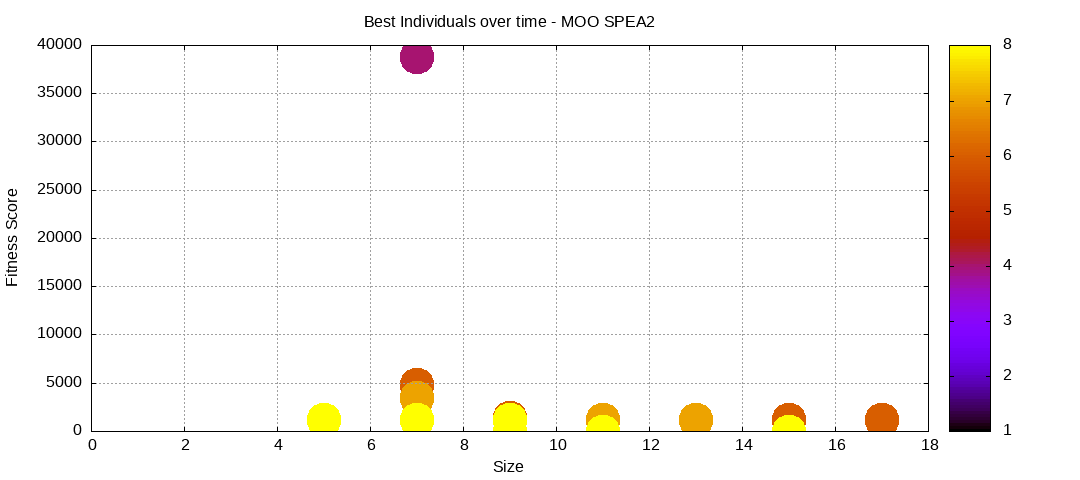
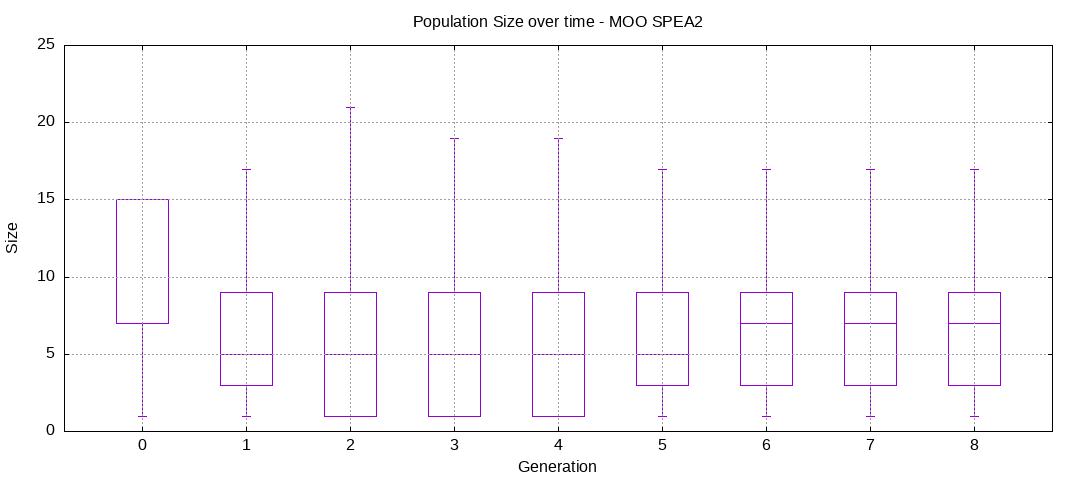
We should observe better fitness over time as well as a containment of the population size.
Conclusion
While this is not an exhaustive assessment and should therefore be considered accordingly, both NSGA2 and SPEA2 have consistently been finding solutions in short amount of steps.
Interestingly, NSGA2 executes faster than SPEA2, but SPEA2 usually finds solutions in a shorter amount of steps. This creates some trade-off where NSGA2 can be used on larger populations or SPEA2 can be used for smaller amount of generations but at a slower speed.
Bloat is an important topic, and for which all these methods demonstrate how a problem could be handled in many different ways.