Fitness Sharing

Introduction

A potential issue with meta-heuristic optimizations such as Genetic Algorithms is to be stuck optimizing a local optimum. There are various ways to deal with it and one of them is called Fitness Sharing.

Fitness Sharing improves the situation by adjusting the fitness of each individual falling within some specified distance using a power law distribution. The adjusted fitness can be described as:

\$F'(i) = {F(i)} / {\sum_{j}^n"sharing"(d(i,j))}\$

Where:

\$F(i)\$ represents the original fitness
\$d(i,j)\$ represents the distance between two solutions in either the genotype or phenotype space. Phenotypes comparisons are usually preferred
\$"sharing"(d)\$ represents the sharing function. Most common implementation is represented as \${(1 - (d / sigma_{share})^alpha if d <= sigma_{share}),("0 otherwise"):}\$

In effect, Fitness Sharing adds a penalty to genotypes being too similar and encourages those being a bit further.

Context

To illustrate Fitness Sharing, we will attempt to find the value of x which maximizes the function \$f(x) = abs(30 * sin(x/10))\$ where \$ 0 <= x <= 100\$

We will compare the solutions we get without and with fitness sharing.

Without Fitness Sharing

Let’s start by defining our EAConfiguration:

final Builder<Double> eaConfigurationBuilder = new EAConfiguration.Builder<>();
eaConfigurationBuilder.chromosomeSpecs(BitChromosomeSpec.of(7))
                .parentSelectionPolicy(Tournament.of(2))
                .combinationPolicy(MultiPointCrossover.of(2))
                .mutationPolicies(RandomMutation.of(0.05))
                .fitness((genotype) -> {
                        final int x = toPhenotype(genotype);
                        return x < 0 || x > 100 ? 0.0 : Math.abs(30 * Math.sin(x / 10));
                })
                .termination(Terminations.ofMaxGeneration(5));
final EAConfiguration<Double> eaConfiguration = eaConfigurationBuilder.build();

This is a standard configuration with a binary representation for our x value and:

a tournament with two participants at each round to select parents
a 2 multipoints crossover
a random mutation on the offsprings with 5% chances

We will also let it run for 5 generations.

Then let’s define an execution context with a population of 50 individuals and some standard loggers, including a CSV logger so we can plot some graphs:

final var csvEvolutionListener = CSVEvolutionListener.<Double, Void>of(csvFilenameWithoutSharing,
                List.of(ColumnExtractor.of("generation", es -> es.generation()),
                                ColumnExtractor.of("fitness", es -> es.fitness()),
                                ColumnExtractor.of("x", es -> toPhenotype(es.individual()))));

final var logTop5EvolutionListener = EvolutionListeners
                .<Double>ofLogTopN(logger, 5, genotype -> Integer.toString(toPhenotype(genotype)));

final EAExecutionContext<Double> eaExecutionContext = EAExecutionContexts.<Double>forScalarFitness()
                .populationSize(populationSize)
                .addEvolutionListeners(logTop5EvolutionListener, csvEvolutionListener)
                .build();

Finally, let’s execute it!

final EASystem<Double> eaSystem = EASystemFactory.from(eaConfiguration, eaExecutionContext);

final EvolutionResult<Double> evolutionResult = eaSystem.evolve();
logger.info("Best genotype: {}", evolutionResult.bestGenotype());
logger.info("  with fitness: {}", evolutionResult.bestFitness());
logger.info("  at generation: {}", evolutionResult.generation());

Now that it has executed, we can plot the results and observe how do the proposed solutions fit in after 5 generations:

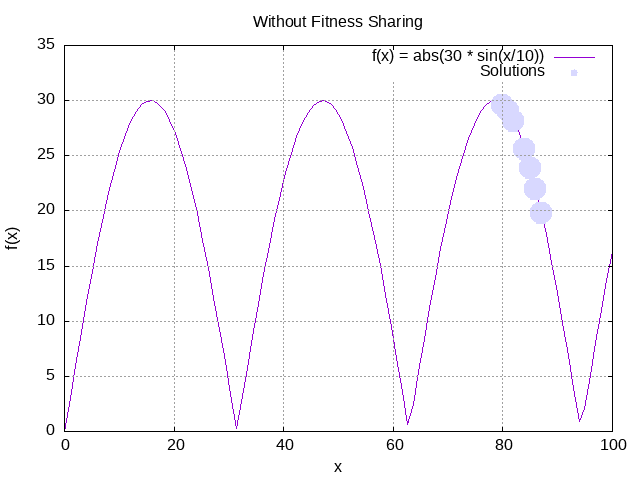
We can already observe some great solutions after 5 generations, but they all gather around a single peak.

With Fitness Sharing

Genetics4j provides some utilities to implement Fitness Sharing in the class aptly named FitnessSharing. It is used as a post evaluation processor which is run after the fitnesses are evaluated.

In order to ensure that both of our cases run with the same configuration (except for the fitness sharing) and to minimize code duplication, we will instantiate an EAConfiguration from the previous case and tweak it to add our fitness sharing:

var eaConfigurationWithFitnessSharing = new EAConfiguration.Builder<Double>().from(eaConfiguration)
                .postEvaluationProcessor(FitnessSharing.ofStandard((i1, i2) -> {

                        final BitChromosome bitChromosome1 = i1.getChromosome(0, BitChromosome.class);
                        final BitChromosome bitChromosome2 = i2.getChromosome(0, BitChromosome.class);

                        return (double) BitChromosomeUtils.hammingDistance(bitChromosome1, bitChromosome2);
                }, 5.0))
                .build();

In this configuration, we do use the hamming distance in the genotype space as a distance measure and set \$sigma_{share} = 5\$.

Next is the creation of an eaExecutionContext with the same configuration, except for the filename of the generated csv file:

final var csvEvolutionListenerWithFitnessSharing = new CSVEvolutionListener.Builder<Double, Void>()
                .from(csvEvolutionListener)
                .filename(csvFilenameWithSharing)
                .build();

final var eaExecutionContextWithFitnessSharing = EAExecutionContext.<Double>builder()
                .from(eaExecutionContext)
                .evolutionListeners(List.of(logTop5EvolutionListener, csvEvolutionListenerWithFitnessSharing))
                .build();

And finally the EASystem and its execution:

final EASystem<Double> eaSystemWithFitnessSharing = EASystemFactory.from(eaConfigurationWithFitnessSharing,
                eaExecutionContextWithFitnessSharing);

final EvolutionResult<Double> evolutionResultWithFitnessSharing = eaSystemWithFitnessSharing.evolve();
logger.info("Best genotype: {}", evolutionResultWithFitnessSharing.bestGenotype());
logger.info("  with fitness: {}", evolutionResultWithFitnessSharing.bestFitness());
logger.info("  at generation: {}", evolutionResultWithFitnessSharing.generation());

We can now plot the results with fitness sharing:

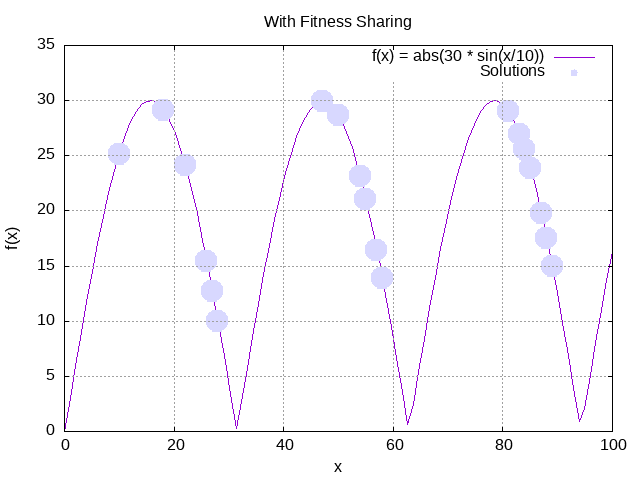
Contrary to our previous run, we can clearly see that the solutions are spread across the different peaks, signaling higher diversity.